TECHNIQUE DE MESURE DES ELEMENTS DIAGONAUX ET NON DIAGONAUX DU TENSEUR DE LA
TURBULENCE AU MOYEN DU SYSTEME RADIOACOUSTIQUE DE SONDAGE DES BASSES COUCHES DE
L'ATMOSPHERE RACES.
Pr. Pierre E. Ravussin, Université Paris 7, 1980
Abstract:
The Radio Acoustic Electronic Sounding system RACES consists of an acoustic
radar with a new geometry coupled to a CW Doppler radar and a minicomputer. The
RACES system measures remotely and continuously the vertical profiles of
temperature, three-dimensional wind vector, diagonal and non-diagonal elements
of turbulence tensor. The diffused sound coming from the same point of
space at the same time is measured by means of three acoustic receivers. The
feasibility of the device is calculated.
Introduction
Principe de mesure
Calcul de faisabilité
Conclusion
Bibliographie
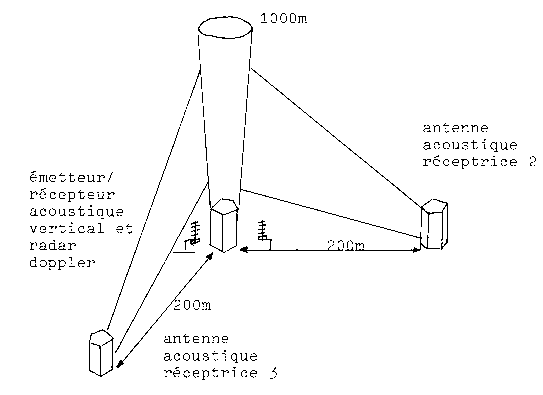
Le système de sondage
radioacoustique RACES est composé d'un sondeur acoustique conçu selon une géométrie
nouvelle, couplé à un radar doppler continu et un mini ordinateur. (Fig. 1)
Il a été développé (1), (2)
jusqu'ici dans le cadre de la Chaire de Mécanique de la Turbulence de l' Ecole
Polytechnique Fédérale de Lausanne et du groupe EPFL-ISM 2) sur
l'environnement atmosphérique. ISM Institut Suisse de Météorologie
Le système RACES mesure en continu
les profils verticaux de la température, des composantes tridimensionelles du
vent moyen et des éléments diagonaux et non diagonaux du tenseur de la
turbulence du vent et de la température.
La partie du système RACES mesurant
la température a déjà fait l'objet de descriptions et d'une campagne de comparaison (3)
Pour obtenir les éléments du tenseur de la turbulence
_______
u’i
u’j i,j = 1,2,3
il est nécessaire
d'obtenir en un même point de l'espace et au même temps les diverses réalisations
umi
i = 1,2,3 ;
m = 1,2, …, µ
des variables
aléatoires ui
i = 1,2,3

Fig.1
Pour respecter
ces conditions, le système RACES émet verticalement une suite d'impulsions
sonores d'une durée d'environ 60ms, qui diffusent sur les tourbillons à petite échelle
de l'atmosphère. Le son ainsi diffusé est capté simultanément (au temps de
vol près), selon trois directions différentes, au moyen de trois antennes
acoustiques réparties dans le terrain. (fig 1).
Connaissant
l'altitude du train d'ondes sonores et la vitesse de propagation du son dans
l'air au moyen du radar Doppler continu, il est possible de grouper les informations
provenant du même point de l'espace et émise donc en même temps en ce point:
uim(P, t) i
= 1,2 3
(nous adaptons ici la convention indicielle du calcul tensoriel)
t
est ici le temps de propagation de l'impulsion sonore de
l'antenne émettrice au point P.
Pour obtenir un ensemble de réalisations
des variables aléatoires, le système RACES émet la série d'impulsions
sonores à intervalle rapproché (env. 4s). Or il a été montré (4) que
l'atmosphère peut être en général considérée comme stationnaire pendant un
intervalle temps de l'ordre de 20
minutes.
Il est donc possible, selon la théorie
ergodique, de considérer une série temporelle de par exemple 300 valeurs comme
représentative de la variable aléatoire ui
(P, t)en
ce point, en un temps contenu dans l'intervalle de mesure.
(t est ici le temps universel), ce qui permet de calculer les moments de divers ordre
__
_____
ui(P, t);
ui uj (P, t)
,
etc.
Mais ce tenseur est calculé dans un
repère non orthogonal, variant avec P. Il faut donc encore
l'appliquer dans un des repères cartésiens utilisé en turbulence au
®
®
u*(P,
t) = A(P) u(P, t)
Pour les moments du 2ème ordre, cette application s'écrit:
_______
______
U*i u*j (P, t) = ail(P) ajm(P)
Ul um (P, t) i,j,l,m = 1,2,3
3.1 Théorie
Selon (6), le coefficient angulaire
de diffusion de l'onde sonore est donné par la relation:
sq = 0,38 k1/3 cos2 q (2 sin q/2)-11/3
[ CV2 e2/3 / C02
cos2 q/2
+ 0,13 CT2/T02]
où
q
angle de diffusion
k nombre d'onde du signal sonore (fixé)
CV
constante caractéristique de la turbulence mécanique
e
taux de dissipation de l'énergie turbulente mécanique
CT
constante caractéristique de la turbulence thermique
C0 vitesse du son dans l'air
T0 température absolue de l'air
Le coefficient de
diffusion est donc composé de deux termes distincts dont l'un provient de la
turbulence mécanique (vent) et l'autre de la turbulence thermique.
Soit sq = sV(q) + sT(q)
sV(q) coefficient
de diffusion angulaire mécanique
sT(q)
coefficient de
diffusion angulaire thermique
avec sV
= KV
cos2 q
(sin q/2)-11/3 cos2
q/2
sT
= KT
cos2 q
(sin q/2)-11/3
KV
coefficient
caractéristique de la diffusion turbulente mécanique
KT
coefficient
caractéristique de la diffusion turbulente thermique
KV
=
0,38 k1/3 CV2
e2/3 / C02
KT
=
0,05 k1/3 CT2/T02
KV et KT caractérisent l'état de turbulence de l'atmosphère.
La loi de
diffusion angulaire du son dans l'atmosphère turbulente diffère s'il s'agit de
turbulence mécanique ou de turbulence thermique.
En particulier, pour la rétro - diffusion (q = 0)
sV
= 0
sT
= KT
Seule la
turbulence d'origine thermique donne un signal rétrodiffusé.
On remarque en outre
que sV
= sT
= 0 pour q
= 0 : il n'y a pas de son diffusé dans une direction perpendiculaire au train
d'ondes sonores.
3.2 Puissance
relative reçue
En supposant que les dimensions du volume du train d'ondes sonores soient petites vis-à-vis de la distance d qui le sépare de l'antenne sonore réceptrice, elle-
3.2 Puissance
relative reçue
En
supposant que les dimensions du volume du train d'ondes sonores soient petites
vis‑à‑vis de la distance d qui le sépare de l'antenne sonore réceptrice,
elle‑même de petite dimension devant d , la puissance sonore relative S'écrit:
[13]
P = sq /d2
en posant
l = distance antenne émettrice ‑ antenne réceptrice
h = hauteur du train
d'ondes sonores
[14] d2 = l2 + h2
On normalise la
puissance relative reçue en posant
k
= h / l et
l
= 1
alors, on défini 3
puissances reçues normalisées.
[15] PV
= cos2 q (2 sin q/2)-11/3 cos2
q/2
/ (k2+1) puissance relative mécanique
[16] PT
= cos2 q (2 sin q/2)-11/3 / (k2+1)
puissance relative
thermique
Et le cas particulier
[17] PR
= 0,078 / k2
puissance
relative rétro - diffusée
thermique
[18] q = p -Arctg 1/k
Les 3 fonctions PV , PT et PR sont reportées sur la figure 2
en tenant compte des données suivantes:
·
la portée pratique d'un sodar monostatique comportant une
antenne acoustique de 120W électrique
est de 1000m
·
l'antenne acoustique moyenne puissance du RACES supporte
1200W électrique
·
l'expérience montre qu'en général KV
>>KT. Nous avons pris KV = 10 KT.
·
la distance antenne émettrice - antenne réceptrice est
de 200m.
On constate que la portée pratique est multipliée par un
facteur 3. L'intensité du signal sonore reçu par les antennes acoustiques latérales
est 20 fois supérieure à la limite de sensibilité.
Entre 200m et 500m,
l'intensité reçue est supérieure à l'intensité rétrodiffusée.
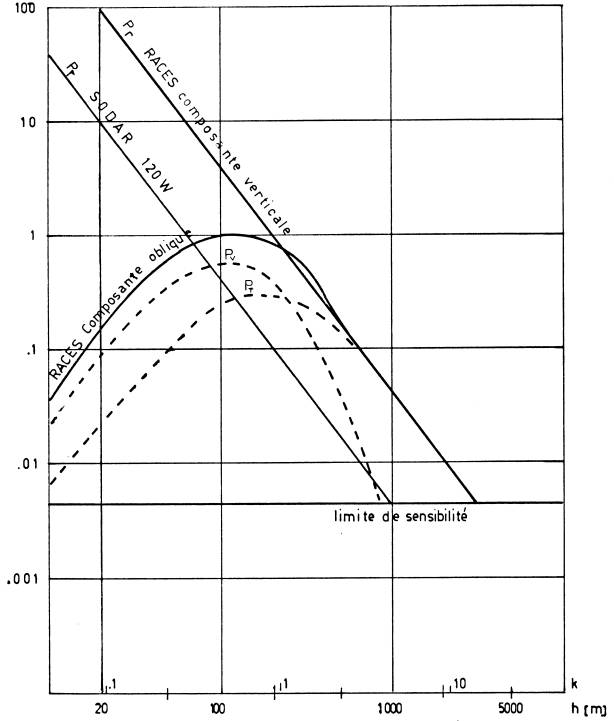
Fig 2
4. Conclusions
Ces caractéristiques
font du système RACES un instrument utile non seulement pour l'étude des
basses couches de l'atmosphère mais aussi pour les travaux de recherche
fondamentale en turbulence tridimensionelle instationnaire et anisotrope.
Comme il fonctionne en
continu, automatiquement et en temps réel, il peut être aussi utilisé pour
les travaux de routine de surveillance de
l'atmosphère, pour
les problèmes de pollution, de sécurité en aviation, etc.
Contrairement aux
autres méthodes utilisée jusqu'ici, le système RACES peut effectuer des
mesures là ou le champ vectoriel du vent est inhomogène, tel que les régions
montagneuses, les littoraux marins, etc.
5. Bibliographie
1.
P. Ravussin, Théorie du Sodar, colloque sur les techniques de mesures
fines de l'atmosphère et mesures à distance, Lausanne 1976, EPFL, PPl‑13
2.
P. Ravussin, Mesures des paramètres météorologiques de l'atmosphère
au moyen d'un radar acoustique, Papers presented at WMO conference on
Instruments and Methods of Observation (TECIMO), Hamburg, 1977, WMO no.480,
PP.159‑164
3.
WMO, Instruments and Observing Methods, Report no.3, Lower Tropospheric
data compatibility, Low Level Intercomparison Experiment, Boulder, 1979,
PP38‑46, 148, 168
4.
Panchev, Random Functions and Turbulence, Pergam.on Press, New York, 1971
5.
P. Ravussin, Les grandeurs aléatoires dans un changement de base,
publication interne CMT 1977
6.
Tatarskii, The Effect of the Turbulent Atmosphere on Wave Propagation,
Keter Press, Jerusalem., 1971
même
de petite dimension devant d , la puissance sonore relative S'écrit:
[13]
P = sq /d2
en posant
l = distance antenne émettrice - antenne réceptrice
h = hauteur du train d'ondes sonores
[14] d2 = l2 + h2
On normalise la
puissance relative reçue en posant
k
= h / l et
l = 1
alors, on défini 3
puissances reçues normalisées.
[15] PV
= cos2 q (2 sin q/2)-11/3 cos2
q/2
/ (k2+1) puissance relative mécanique
[16] PT
= cos2 q (2 sin q/2)-11/3 / (k2+1)
puissance relative
thermique
Et le cas particulier
[17] PR
= 0,078 / k2
puissance
relative rétro - diffusée
thermique
[18] q = p -Arctg 1/k
Les 3 fonctions PV , PT et PR sont reportées sur la figure 2
en tenant compte des données suivantes:
la portée pratique d'un sodar monostatique comportant une antenne acoustique de 120W électrique est de 1000m
l'antenne acoustique moyenne puissance du RACES supporte 1200W électrique
l'expérience montre qu'en général KV >>KT. Nous avons pris KV = 10 KT.
la distance antenne émettrice - antenne réceptrice est
de 200m.
On constate que la portée
pratique est multipliée par un facteur 3. L'intensité du signal sonore reçu
par les antennes acoustiques latérales est 20 fois supérieure à la limite de
sensibilité.
Entre 200m et 500m,
l'intensité reçue est supérieure à l'intensité rétrodiffusée.
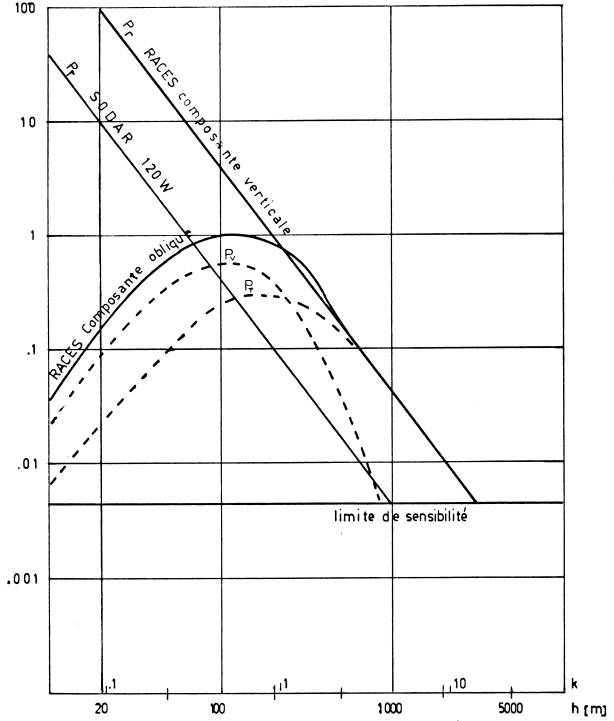
Fig 2
Ces caractéristiques
font du système RACES un instrument utile non seulement pour l'étude des
basses couches de l'atmosphère mais aussi pour les travaux de recherche
fondamentale en turbulence tridimensionelle instationnaire et anisotrope.
Comme il fonctionne en
continu, automatiquement et en temps réel, il peut être aussi utilisé pour
les travaux de routine de surveillance de l'atmosphère, pour les problèmes de
pollution, de sécurité en aviation, etc.
Contrairement aux
autres méthodes utilisée jusqu'ici, le système RACES peut effectuer des
mesures là ou le champ vectoriel du vent est inhomogène, tel que les régions
montagneuses, les littoraux marins, etc.
1.
P. Ravussin, Théorie du Sodar, colloque sur les techniques de mesures
fines de l'atmosphère et mesures à distance, Lausanne 1976, EPFL, PPl‑13
2.
P. Ravussin, Mesures des paramètres météorologiques de l'atmosphère
au moyen d'un radar acoustique, Papers presented at WMO conference on
Instruments and Methods of Observation (TECIMO), Hamburg, 1977, WMO no.480,
PP.159‑164
3.
WMO, Instruments and Observing Methods, Report no.3, Lower Tropospheric
data compatibility, Low Level Intercomparison Experiment, Boulder, 1979,
PP38‑46, 148, 168
4.
Panchev, Random Functions and Turbulence, Pergam.on Press, New York, 1971
5.
P. Ravussin, Les grandeurs aléatoires dans un changement de base,
publication interne CMT 1977
6.
Tatarskii, The Effect of the Turbulent Atmosphere on Wave Propagation,
Keter Press, Jerusalem., 1971
(A suivre)